Файл:Pm1234 Euler.svg
Исходный файл (SVG-файл, номинально 240 × 390 пкс, размер файла: 26 Кб)
Этот файл из на Викискладе и может использоваться в других проектах. Информация с его страницы описания приведена ниже.
Краткое описание
| ОписаниеPm1234 Euler.svg |
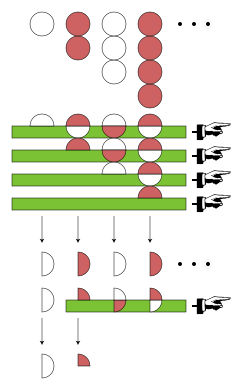
English: Euler summation of 1 − 2 + 3 − 4 + · · · to 1/2-1/4.
The original series 1 − 2 + 3 − 4 + · · · is depicted at the top of the diagram; the Euler transformed series 1/2 − 1/4 + 0 + 0 + · · · is depicted at the bottom of the diagram. The conclusion is that the Euler sum of 1 − 2 + 3 − 4 + · · · is 1/2-1/4 = 1/4. Only the first four terms of the series are shown. A white disk represents +1; a reddish disk represents −1. The units are grouped on top of each other as they occur within the terms of the series. Let a = 1 − 2 + 3 − 4 + · · · be the original formal series. Let S be the shift operator on formal series, Let T be the average between S and the identity operator: Then given a series a, if it converges, then its sum is the same as the sum of the series The Euler summation procedure has many descriptions, but for the present purposes it can be described as a repetition of the above "process". To be precise, the nth term of the Euler transformed series is See eq. (20.3) of Korevaar, Jacob (2004) Tauberian Theory: A Century of Developments, Springer, стр. 326 ISBN 3-540-21058-X To compute this transform in place, one pulls half of each term into the next term, then fixes the first term, then repeats. The part of the diagram with the four green stripes indicates taking half of every term in the original series a and pulling it into the next term. Most of the units cancel, leaving the series The first term of this series is fixed, leaving The process repeated upon the remaining terms, leaving 1/2 − 1/4 + 0 + 0 + · · ·. Now two terms are fixed, and the remaining terms are all zero, so all further applications of T do not change the series, and they are not depicted. In the visual language, subsequent green stripes pull on nothingness. The result is the Euler transformed series, 1/2 − 1/4 + 0 + 0 + · · ·. It is convergent, having only two nonzero terms, and its sum is 1/2 − 1/4. The diagram does not distinguish between the finite series and its sum. As a number, 1/2 − 1/4 = 1/4. The above is done to illustrate how Euler summation works on the series. In practice, one exploits auxiliary quantities, and the computation is much easier; see for example Image:Pm1234-Euler1755.png. An extended description of Euler's procedure on 1 − 2 + 3 − 4 + · · ·, including reversing its alternation and taking iterated forward differences, is at w:1 − 2 + 3 − 4 + · · ·#Euler and Borel. |
| Дата | |
| Источник | User created |
| Автор | User:Melchoir |
| Другие версии | PNG version |
Лицензирование

|
Разрешается копировать, распространять и/или изменять этот документ в соответствии с условиями GNU Free Documentation License версии 1.2 или более поздней, опубликованной Фондом свободного программного обеспечения, без неизменяемых разделов, без текстов, помещаемых на первой и последней обложке. Копия лицензии включена в раздел, озаглавленный GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
| Этот файл доступен по лицензии Creative Commons Attribution-Share Alike 3.0 Unported. | ||
| ||
| Этот признак лицензирования был добавлен к этому файлу как часть обновления лицензии GFDL.http://creativecommons.org/licenses/by-sa/3.0/CC BY-SA 3.0Creative Commons Attribution-Share Alike 3.0truetrue |
- Вы можете свободно:
- делиться произведением – копировать, распространять и передавать данное произведение
- создавать производные – переделывать данное произведение
- При соблюдении следующих условий:
- атрибуция – Вы должны указать авторство, предоставить ссылку на лицензию и указать, внёс ли автор какие-либо изменения. Это можно сделать любым разумным способом, но не создавая впечатление, что лицензиат поддерживает вас или использование вами данного произведения.
- распространение на тех же условиях – Если вы изменяете, преобразуете или создаёте иное произведение на основе данного, то обязаны использовать лицензию исходного произведения или лицензию, совместимую с исходной.
Краткие подписи
Элементы, изображённые на этом файле
изображённый объект
4 марта 2007
История файла
Нажмите на дату/время, чтобы увидеть версию файла от того времени.
| Дата/время | Миниатюра | Размеры | Участник | Примечание | |
|---|---|---|---|---|---|
| текущий | 13:43, 1 января 2008 |  | 240 × 390 (26 Кб) | wikimediacommons>Papa November | Removed unnecessary Adobe Illustrator metadata. May fix rendering problems. No copyright claimed for non-creative derivative work. |
Использование файла
Следующая страница использует этот файл:




